Ruta de esta página: Curso de demografía / Temario / Tema 4: Análisis de la mortalidad /
Pueden verse ejemplos de tablas de mortalidad y cálculo de la esperanza de vida en los ejercicios resueltos (los números 4 y 4c)
La esperanza de vida es un concepto que sólo tiene sentido para una generación y se obtiene como parte de una tabla de mortalidad. La generación puede ser real, o puede ser una generación hipotética que, como columna de probabilidades de morir (qx), tiene los datos de un cierto año o periodo, no los de una auténtica generación. En este caso, lo que se hace en realidad es averiguar «cual sería la esperanza de vida de una generación que, a lo largo de sus sucesivas edades, fuese extinguiéndose con una mortalidad como la de ese año o periodo». Incluso en este segundo caso, constituye un indicador sobre la «fuerza»de la mortalidad, en un periodo histórico concreto, mucho más afinado que la simple tasa bruta de mortalidad (entre otras ventajas, no se ve afectado por los efectos de estructura por edades).
Si se trata de cálculos para una generación real, estaríamos haciendo un análisis longitudinal de su mortalidad, mientras que las tablas de mortalidad construidas con datos «de momento» forman parte de lo que llamamos análisis transversal del fenómeno.
En definitiva, se trata de repartir el conjunto de años de vida vividos por un cierto colectivo inicial para averiguar el número medio de años que corresponde a cada individuo de dicho colectivo. Por tanto, el primer paso es calcular el número total de años vividos por la generación a partir de cierta edad (x). Lo más frecuente es que se calcule desde el nacimiento, es decir, cuando x=0. El promedio se obtiene simplemente repartiendo ese total de años vividos a partir de cierta edad entre la población inicial de dicha edad.
*
donde
Tx es el número total de años vividos desde la edad x
lx son los supervivientes en la edad exacta x
*
Los datos necesarios para aplicar esta fórmula son los de la tabla de mortalidad, con las columnas qx, lx , dx ya desarrolladas. Se trata, por tanto, de calcular una columna adicional que nos diga, para cada edad exacta, cual es el número total de años vividos desde esa edad en adelante (Tx). Generalmente eso se consigue con una columna previa, la de los «años vividos en el intervalo de edad» (Lx), cuyo sumatorio desde la edad x arroja el total de años vividos de esa edad en adelante.
No obstante, es posible el cálculo directo exclusivamente a partir de la columna de supervivientes, lx:
–
Cálculo de la esperanza de vida (ex ) exclusivamente a partir de los datos de supervivientes ( lx )
–
Una primera aproximación al cálculo es la que considera que a todas las defunciones (dx) producidas en cada edad simple se les puede atribuir el haber vivido medio año, como promedio, en ese intervalo de edad (algunas se habrán producido a los pocos días de cumplir la edad en cuestión, otras ya pasados los once meses y, si se suponen repartidas linealmente, considerar que el promedio de todas ellas arroja medio año vivido es una aproximación bastante buena).
Bajo ese supuesto, el número de años vividos a partir de una edad exacta (x) se obtiene de la siguiente manera:
*
*
Si se hace de 0,5 factor común la fórmula puede simplificarse de la siguiente manera:
*
*
y, puesto que el sumatorio de las defunciones a partir de cierta edad es equivalente al efectivo inicial (supervivientes) de dicha edad, la sustitución deja la fórmula así:
*
*
Si volvemos a la fórmula 1, e introducimos la equivalencia de la Tx que acabamos de desarrollar, el resultado es
*
*
y de ello resulta
*

*
Finalmente, y puesto que las defunciones de cada edad equivalen a la diferencia entre los supervivientes al inicio y al final de dicha edad
*
*
lo que equivale, si se hacen las multiplicaciones, a
*
*
y, finalmente,
*
CÁLCULO ABREVIADO
–
La fórmula anterior es de aplicación en las tablas completas de mortalidad, en las que se tienen valores para todas las edades simples. En caso de que la tabla disponible sea sólo una tabla abreviada, deben tenerse en cuenta las amplitudes de los intervalos entre edad.
Lo más corriente son las tablas con intervalos quinquenales pero con especificación de la mortalidad del primer año y de los cuatro siguientes, así como un intervalo abierto al final (P. Ej. 85 y m ás). Suponiendo que se cumple en todos los intervalos de edad la distribución lineal de las defunciones, los niños muertos antes de 1 año vivirían un promedio de 0.5, los fallecidos en las cuatro edades siguientes vivirían un promedio de 2 años, y los restantes un promedio de 2,5 (en cambio los supervivientes al empezar el intervalo abierto vivir án un número medio de años de vida que habrá que obtener por otros medios o que se puede suponer de forma aproximada, puesto que el impacto de su determinación sobre el ajuste final de los resultados es escaso, especialmente cuando se calcula esperanza de vida al nacer).
Si la tabla abreviada sólo tuviese intervalos de cinco años, el cálculo se obtendría así:
*
*
Pero en el caso más frecuente, cuando tenemos datos para el primer año de vida y los cuatro siguientes, el c álculo de e1 y de e0 es distinto:
*
*
Y en el caso de la esperanza de vida al nacer
*

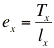


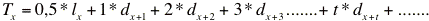







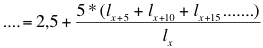


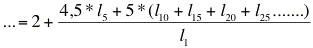



Cual sería la formula para resolver la probabilidad que un recién nacido sobreviva por lo menos 60 años , funciones biometricas aplicando la tabla de mortalidad CSO 1958
Me gustaMe gusta
) Observa los datos siguientes sobre una comunidad:
▪ Población total 150.000 habitantes
▪ Defunciones en un año 72
▪ Defunciones de menores de 50 años 12
▪ Defunciones de menores de 1 año 3
▪ Defunciones por embarazo, parto y puerperio 3
▪ Nacidos vivos 130
▪ Edad media de fallecimiento en mujeres 77,4
▪ Edad media de fallecimiento en hombres 74,8
▪ Casos diagnosticados de tos ferina 30
Calcula los siguientes indicadores: tasa de mortalidad general, esperanza de vida al
nacimiento para hombres y mujeres, tasa de mortalidad infantil, tasa de natalidad, tasa de
mortalidad materna, y tasa de morbilidad (prevalencia) para la tos ferina.
Me gustaMe gusta
Hallar la probabilidad de que un hombre de 40 años de edad no alcance a cumplir los 48 años.
Me gustaMe gusta
Cual es la probabilidad de vida a los 75 años
Me gustaMe gusta
Tengo 78 años. Cuál es mi esperanza de vida.Soy mujer muy sana
Me gustaMe gusta
Creo que sobrevivo 2 años a la expectativa de vida en Colombia.
Me gustaMe gusta
No entendi nada muchas gracias!!!!😎🤙🏼
Me gustaMe gusta
Si en el cálculo de la esperanza de vida, afectan los muertos por accidentes de todo tipo, esto puede confundir mucho a la población.
Dado que puede haber grandes catástrofes en una zona y bajar la esperanza de vida.
Si ésto es así Para mí el cálculo sería erróneo.
Ya que los datos de esperanza de vida habiendo habido un terremoto en un país con escasa población ( por ejemplo) daría una esperanza de vida no real ( a menos que hubiera terremotos cíclicos con el mismo número de afectados todos los años.
Me gustaMe gusta
Buenos dias, mi pregunta es la siguiente, existe alguna formula que relacione la esperanza de vida con la esperanza de vida de otro año?. Ejemplo, si se la esperanza de vida de 30 años y me pden la de 0 años… existe alguna formula, por supuesto conociendo la población ficticia desde los 0 a la de 30 años….
Me gustaMe gusta
POR FAVOR AYUDA.
necesito profundizar en el tema de «ESPERANZA DE VIDA ABREVIADA Y COMPLETA»
En el documento está fórmula: ex= E(K)
La desarrollan y terminan en una igualdad con Inegrales.
EL otro tema es » VIDA PROBABLE»
rpx=rqx=1 /2
No encuentro más información.
Si alguien tiene información sobre esto por favor que me comparta.
Me gustaMe gusta
Entendiendo la esperanza de vida como la media de la edad de las personas de una población que mueren en un determinado período, no encuentro relación en su cálculo con la edad media de una población. Sin embargo, suponiendo dos poblaciones, una con edad media, por ejemplo, 60, y una segunda con edad media 70, pues tiendo a pensar que la esperanza de vida será mayor en la segunda población. Aún así, no he sido capaz de demostrarlo y encontrarle el razonamiento matemático.
Agradecería ayuda si fuese posible. Gracias de antemano, y por las publicaciones detalladas y completas!
Me gustaMe gusta
Hola Irene, gracias por escribir el comentario. Hay algún docente que está confundiendo a sus alumnos al afirmar que la esperanza de vida se calcula sobre una población real, y que es la edad media de los fallecidos de un cierto año o, por aún, que guarda relación con la edad media de sus habitantes. Es un error grave, porque el cálculo debe hacerse sobre una tabla de mortalidad, no sobre la población, y no es la edad media de la población (eso podría calcularse sin tener ningún dato sobre su mortalidad), sino el número medio de años que viviría una generación ficticia que se fuese muriendo por edades con las probabilidades de morir de ese año. LA ESPERANZA DE VIDA NO GUARDA NINGUNA RELACIÓN CON LA EDAD MEDIA DE LA POBLACIÓN. La edad media de la población puede verse afectada por las migraciones o por la natalidad más o menos alta, mientras que la tabla de mortalidad es independiente de todos esos fenómenos y también de la pirámide de edades. No es cuestión de cálculo, sino de concepto. Una tabla de mortalidad simula la progresiva extinción de una generación. La tabla de supervivientes a cada edad no tiene nada que ver con el número de habitantes real de esa población en cada edad. En una población real puedes tener más personas de 50 años que de 15, y también puedes tener muchos fallecidos en cierta edad simplemente porque en esa edad hay mucha más gente que en otras edades. Pero en una tabla de mortalidad nunca tendrás más supervivientes a los 50 que a los 15 o que a ninguna edad anterior, por la sencilla razón de que siempre se trata de las mismas personas que, progresivamente, van muriendo, no resucitan. Tienes aquí material tutorial y ejercicios resueltos en los que se calcula la esperanza de vida, échales un vistazo https://apuntesdedemografia.com/curso-de-demografia/temario/tema-4-analisis-de-la-mortalidad/ . De hecho la mejor manera de entenderlo es intentar resolver alguno de los ejercicios.
(y pídele a tu profesor, si la confusión viene de sus explicaciones, que desvincule esperanza de vida y edad media). Un saludo, espero haber aclarado tus dudas, gracias de nuevo por escribir.
Me gustaMe gusta
Entonces, a una cuestión como la siguiente:
“Edad media en población 1 es de 50 años y en 2 es de 55 años, ¿en cuál de ellas sería mayor la esperanza de vida? “
¿La respuesta sería que no se puede afirmar nada pues no existe ninguna relación entre la edad media de la población y la esperanza de vida en la misma?
Muchas gracias!
Me gustaMe gusta
En efecto. Una población puede tener una edad media más alta porque han emigrado los jóvenes, o porque se ha construido un geriátrico y ahora está lleno de gente mayor con origen en muchos otros sitios. La historia de una pirámide se construye a lo largo de muchas décadas y muchas generaciones y no es una historia cerrada. Saludos!
Me gustaMe gusta
Hola a mi hija le colocaron esta taera pero no entiendo exactamente lo que hay que hacer alguien me ayuda a resolverla dice analizar mi expectativa de vida ( datos estadisticos)
Me gustaMe gusta
Hola, me gustaría saber si hay alguna fórmula diferente, y si la habéis publicado en esta web, ya que en mi libro de la facultad dice que la fórmula es la siguiente: Suma de los años vividos por los miembros de una población/ No de individuos de esa población.
Muchas gracias,
Un saludo
Me gustaMe gusta
Hola Mariana. Antes de contestar, una aclaración: no «hemos publicado» porque la web no es colectiva, es personal. Me llamo Julio y es un placer ayudar si está en mi mano. Respecto a la pregunta, la respuesta es simple; no hay diferencia entre los «miembros» y los «individuos» de esa población, la fórmula no va a cambiar porque se use una u otra expresión, igual que si en otro libro leyeses «los componentes», o «las personas», o «los integrantes». De hecho las fórmulas no usan palabras, sino variables en forma de letras, así que la fórmula es la misma, no cambia por usar una palabra u otra. Gracias por escribir y un saludo muy cordial.
Me gustaMe gusta
Y para completar la respuesta, tu libro de la facultad usa la misma fórmula, pero emplea mal la expresión que define el denominador. La esperanza de vida se calcula siempre mediante una tabla de mortalidad, y la población del denominador va cambiando después del nacimiento a medida que van falleciendo personas. Tu manual debería aclarar que habla de la esperanza de vida al nacer, pero la fórmula que os proporciono es general, y sirve para calcular la esperanza de vida a cualquier edad, incluyendo la edad cero, claro.
Me gustaMe gusta
hola, necesito calcular la edad de una persona que tiene una esperanza de vida de 14,3 años, ¿esta formula me sirve?.
Me gustaMe gusta
Hola Mauro, gracias por escribir. Lo que quieres calcular requiere más información que la que escribes. De hecho sólo se puede responder en función de una tabla de mortalidad completa y concreta. En otras palabras, para calcular la edad de alguien sabiendo su esperanza de vida tienes que hacerlo sobre una población y sobre un año concretos, para los que dispongas de toda la tabla de vida, de manera que la respuesta a tu pregunta es distinta en Alemania que en Australia, y es distinta en la Alemania de 1019 o la de 1919. Siento no ser de más ayuda, muchos saludos
Me gustaMe gusta
Efectivamente resulta muy complejo de entender por lo que para mi una persona que no tiene una formación profesional especializada en el tema pero para quien resulta de interés por el tipo de actividad a la que me dedico, mi pregunta es, si la esperanza de vida es generacional, en un espacio y tiempo determinado y se revisa trienalmente, puedo entender que se mezclan los cálculos a partir de la generación de la que se darán los datos con los datos de generaciones anteriores en ese territorio y que se incluyen en los datos de mortalidad de estas generaciones?
Gracias
Me gustaMe gusta
Hola Lilia, gracias por escribir. Tienes que disculparme si no entiendo bien tu pregunta y te pido que la detalles un poco más. De todas maneras estás comentando probablemente la página más técnica y matemática sobre la tabla de mortalidad. En esta web tienes otras páginas más fáciles sobre la tabla y la esperanza de vida, incluyendo ejercicios resueltos sobre la manera de hacer los cálculos, y a lo mejor te resultan útiles: https://apuntesdedemografia.com/curso-de-demografia/temario/tema-4-analisis-de-la-mortalidad/
Me gustaMe gusta
Hola, tengo un pregunta: la esperanza de vida es más alta ahora en Europa que hace unas décadas, y eso se interpreta y publicita como un aumento en la salud de la población ¿puede ser que no sea por una mejora de la salud, sino simplemente por la ausencia de guerras y de fallecimientos a causa de las guerras desde 1945 -salvo la guerra de los Balcanes en los 90?
Me gustaMe gusta
Hola Beatriz, tu pregunta tiene mucho sentido. De hecho, hasta prácticamente el siglo XX, la humanidad entera ha arrastrado tres grandes tipos de crisis de sobremortalidad, las hambrunas, las guerras y las epidemias. Eran tan recurrentes y frecuentes que formaban parte de los lastres «sistémicos» para una esperanza de vida que nunca en ningún lugar superó los 35 años. Pero la otra mortalidad, la «ordinaria», tampoco daba para mucho más, especialmente por la mortalidad temprana (la mitad de los nacidos no llegaban a los 15 años con vida). Los demógrafos históricos creen que el primer gran cambio lo produjo un espaciamiento cada vez mayor de las crisis, y luego, sobre todo, el descenso de la mortalidad infantil. En realidad incluso las dos guerras mundiales fueron ya incapaces de detener el gran impulso que estaba experimentando la esperanza de vida en Europa y en el mundo entero, al margen ya de las crisis. No es sólo una mejora médica o sanitaria, tiene que ver con muchos otros factores, como la higiene, la alimentación infantil, la mejora en el acceso a alimentos que supuso el ferrocarril o el barco a vapor, o la progresiva escolarización, que apartaba a la infancia de la explotación laboral temprana. Por dramáticas que sean las guerras, sus efectos son históricamente puntuales, pero el resto de factores y su mejora son mucho más importantes y duraderos. Incluso la guerra de los Valcanes produjo poco más que un ligero estancamiento en la esperanza de vida de los países de la antigua Yugoslavia. Saludos y gracias por usar ApdD.
Me gustaMe gusta
Gracias por la respuesta, poseo las tablas de mortalidad que las Superintendencias del Gobierno de Chile publico el año 2015 para el calculo de rentas vitalicias y de retiro programado. Dicha publicación informa de un aumento en la esperanza de vida al jubilar tanto para hombres como para mujeres, en comparación con las tablas anteriores. Sin embargo los valores que publicaron son diferentes a los que logro obtener aplicando la formula anterior. He investigado las tablas que publicaron, en donde los «qx» están suavizados mediante diferentes modelos probabilistico, considerando esto, al aplicar directamente la formula de la esperanza de vida a las tablas de mortalidad completa, debería obtener los mismos resultados que la Superintendencia informo en su comunicado de prensa. Esto ultimo no sucede, y he repasado varias veces el calculo en Excel, ¿Por qué difieren los resultados?, ¿hay otras formulas para calcular la esperanza de vida?. De todas maneras me gustaría saber si tiene algún articulo, en el cual explique esta formula, para poder citarlo, ya que me ha sido de gran utilidad. Espero su respuesta, gracias.
Me gustaMe gusta
Ignoro el motivo de las diferencias entre tus cálculos y las cifras oficiales. El método por el que los estadísticos calcularon las qx no debería importar, porque una vez se tiene esa columna el resto de los cálculos es siempre el mismo. Hay otras fórmulas, claro está, pero prueba a hacer la tabla ignorándolas, sólo calculando la tabla completa columna a columna, como en los ejercicios resueltos (especialmente el 4c), a ver si esta vez los resultados coinciden. Y puedes encontrar más documentación en esta parte de ApdD: https://apuntesdedemografia.com/curso-de-demografia/temario/tema-4-analisis-de-la-mortalidad/ Ya me contarás cómo te va. Saludos
Me gustaMe gusta
hola, desarrolle las columnas «dx», «lx», «Lx» y «Tx», pero tengo una duda en el calculo de «Lx», ya que las tablas de mortalidad tienen la probabilidad de morir para cada edad. Por lo que utilice un valor de «n» = 1. ¿Entonces Lx= lx + dx/2?, con la formula anterior obtuve resultados mas cercanos a las publicaciones de la Superintendencia, pero no idénticos, sin embargo las diferencias son decimales. Por otra parte es extraño que la formula directa de la esperanza de vida arroje resultados distintos.
Me gustaMe gusta
necesito calcular la expectativa de vida de una persona que murio a los 64 años por accidente de trafico
Me gustaMe gusta
¡Ya tienes un buen motivo para aprender cómo funcionan las tablas de mortalidad! Aquí tienes todo lo necesario, las fórmulas y algunos ejemplos prácticos resueltos. El primer paso, claro, es que consigas los datos de mortalidad por edades de la población a la que te refieras. Eso sí, lo que calcularás no es la expectativa de vida de una persona que falleció (lógicamente no tiene ninguna, y tampoco tiene nada que ver si el motivo fue un accidente o cualquier otra causa), sino la que tenían las personas de 64 años en ese momento. Tienes que calcular la columna de años vividos a partir de una edad Tx, y también la de supervivientes en cada edad lx ( ex= Tx/lx en este caso e64= T64/l64). Adelante y gracias por tu interés.
Me gustaMe gusta
no entendi !
Me gustaMe gusta
Es normal, no te preocupes demasiado, a mí también me pasó las primeras veces. Lo prioritario no es entenderlo, sino practicarlo con datos reales en una hoja de cálculo. En cualquier ciencia aplicada la comprensión y la práctica van juntas, no basta con recibir muchas indicaciones, fórmulas y teorías, porque después hay que encontrarse ante el caso real y resolver, y eso sólo se hace con la práctica. Tienes esa posibilidad en la página de ejercicios resueltos; puedes practicar con los ejercicios 4, 4a y 4b, seguro que entenderás un poco más. Gracias por usar ApdD y ánimo con los números.
Me gustaMe gusta
Hola, gracias por la publicación. Tengo una duda, la formula para calcular la esperanza de vida a partir de los supervivientes (lx), es posible emplearla teniendo solo las tasas de mortalidad para cada edad, y escogiendo un valor arbitrario para los supervivientes iniciales?
Me gustaMe gusta
En efecto, el número de supervivientes iniciales es arbitrario, puede elegirse el que se quiera, y eso no alterará los indicadores principales de la tabla, como la esperanza de vida. Lo realmente importante son los valores que adopta la columna de probabilidades de morir para cada intervalo de edad (cuidado, no son tasas; con una tabla de tasas por edad habría que hacer la conversión a probabilidades antes de poder construir el resto de la tabla de mortalidad). Tienes aquí algún ejercicio resuelto, y es fácil hacer la prueba, una vez construida la tabla en Excel; puedes sustituir l0 y verás cómo cambian todos los demás valores en columnas como la de defunciones, años vividos, etc., pero las esperanzas de vida se quedan igual
Me gustaMe gusta