En demografía, como en muchas otras disciplinas estadísticas y sociales, es muy corriente expresar relaciones entre dos magnitudes en forma de porcentajes o «tantos por ciento» (también en «tantos por mil», «tantos por cien mil», etc.). El cálculo del porcentaje es muy elemental, pero esta web es para personas muy variadas, muchos sois estudiantes de primeros ciclos, y ya he recibido varias comentarios con preguntas sobre la manera de hacer ese cálculo. Un ejemplo es la consulta de Jesi:
me dieron para calcular unos porcentajes pero no se como hacerlos dice que en 1810 habia 44.800 habitantes y el 3% eran mestizos, el 2%indios, 70%blancos, 25%negros. Cómo sacar la cantidad de habitantes indios, blancos, mestizos y negros ….????? me podrian ayudar se los agradeceria …
(Por cierto, esta pregunta utiliza una clasificación racial muy arcaica y demostradamente falsa; ya era inútil en el siglo XVI, cuando la clasificación de «razas» en las colonias americanas tuvo que ampliarse notablemente a causa de la diversidad generada por la combinación de etnias, pero es que además la genética de las poblaciones actual desmiente su carácter científico y, en general, el propio concepto de «raza humana»; mira en El retrato de castas).
He pensado que la respuesta puede servir a muchos otros de los que usáis ApdD, alumnos o docentes, así que esta entrada es para explicar 1) el procedimiento para hacer el cálculo, pero también, 2) algunas ideas que permiten entender el procedimiento.
Cómo se calcula el porcentaje
El tanto por ciento (A %) de cualquier cantidad (C) se calcula multiplicando esa cantidad C por el número A del porcentaje, y dividiendo el resultado por 100. (A% de C = C*A/100).
En realidad estamos haciendo una simple multiplicación de dos números, porque el porcentaje también puede escribirse como un número fraccionario de este tipo : A/100, que es el número que usamos para multiplicar la cantidad C : C * A/100.
El signo * sustituye aquí al habitual «x» de la multiplicación aritmética, porque cuando se usan expresiones con «incógnitas», como en las ecuaciones, las letras se reservan para nombrarlas, como en y=2x.
Así que, respondiendo a Jessi, el 3% de 44.800 habitantes se calcula multiplicando 44.800 x 3 = 134.400, y ahora, dividiendo por 100, 134.400 / 100 = 1.344
Puede resultarte útil la regla memorística de que al multiplicar o dividir por 10 o por múltiplos de 10 (100, 1000, etc.), en vez de hacer la operación, basta con desplazar la coma a la derecha o la izquierda tantos espacios como ceros tiene el multiplicador o el divisor. Por eso 134.400 dividido por 100 resulta en el mismo número sin los dos últimos ceros.
De la misma manera, el 70% se obtiene así: 44.800 x 70 = 3.136.000, que dividido por 100 resulta 31.360.
Prueba por tu cuenta a calcular los otros dos porcentajes de Jesi, y comprobarás que el 2% son 896 habitantes, y que el 25% son 11.200
Nota: si en vez de tantos por ciento hablamos de tantos por mil, por diez mil, etc,, el procedimiento es idéntico:
70‰ de 44.800 se obtiene así: 44.800 *70 y dividido por 1000= 3.136
LA «REGLA DE TRES»
Al calcular un porcentaje usamos un truco muy antiguo conocido como «regla de tres», que en realidad sirve para calcular muchas otras cosas. En una regla de tres sabemos la proporción que guardan entre sí dos números, a – b, y lo que nos preguntamos es cómo conseguir una pareja para un tercer número c de manera esta c y su pareja guarden la misma relación que tenían a y b. Esto, que suena un poco complicado, se ve mejor con un ejemplo:
a) Todas las oficinas de una empresa guardan una relación de 4 a 1 entre administrativos y analistas, ¿cuántos analistas tiene la sede de Lima, que cuenta con 40 administrativos, para que se mantenga la relación constante de 4 a 1?
Si este ejemplo no te parece claro, seguro que este otro te parecerá algo mejor:
b) Por cada 2 cucharadas de azúcar hay que añadir 3 de harina. Cuántas cucharadas de harina habré usado si puse 10 de azúcar.
En ambos casos el esquema es el mismo
-
- 4 admin /1 analis —> 40 admin/? analis
- 2 azuc / 3 harina —> ? azuc / 15 harina
Ese número que no conocemos y que he escrito con un interrogante es lo que en álgebra se conoce como la «incógnita» de una ecuación, la «x«, así que también podemos escribir las relaciones de arriba de esta manera
- 4/1 = 40/x
- 2/3 = x/15
Pero en una ecuación la igualdad se mantiene si un número que está multiplicando o dividiendo a la «incógnita» se traslada al otro lado de la igualdad pero haciendo la operación contraria (si multiplicaba pasa dividiendo, y si dividía pasa multiplicando). Así que las dos incógnitas de arriba se resuelven así:
- (4 /1)*x= 40 —-> x= 40/(4/1) —-> x= 10
- 2*15 /3 = x —-> x= 30/3 = 10
En otros términos, con estas dos soluciones puedes comprobar que se cumple
- 4/1 = 40/10
- 2/3 = 10/15
Cuando se calcula un porcentaje se está haciendo exactamente lo mismo; nos preguntamos qué número tenemos que relacionar con una cantidad para que guarden la relación del porcentaje. En el ejemplo de Jesi se pretende saber qué numero de mestizos hay en una población de 44.800 habitantes para que resulten el 3% . Aplicando el mismo esquema anterior
3/100 = x / 44.800
así que pasamos el dividendo al otro lado multiplicando y nos resulta
3*44.800 / 100 = x
x = 3*44.800 / 100 = 134.400/100 = 1.344
como ya habíamos visto arriba.
QUÉ ES UN PORCENTAJE Y POR QUÉ SE CALCULA ASÍ
Los números fraccionarios se construyen dividiendo dos números enteros a/b . Os recuerdo algunas cosas básicas sobre los tipos de conjuntos de números que se utilizan para empezar a construir las matemáticas.
- números naturales: son los que «cuentan» cosas (dos coches, cuatro ruedas, mil tornillos…), y configuran, cada uno de ellos, el conjunto de cosas contadas con el mismo resultado. Así el número 2 sirve para nombrar el conjunto de veces que la cuenta nos da esa cantidad (dos coches, dos lápices, dos personas…).
- números enteros: son los que resultan de restar un número natural a otro (a-b), así que pueden ser positivos o negativos ( 3-2=+1 ; 2-3=-1 ). También son un conjunto, porque cada número entero representa una cantidad infinita de pares de números naturales restados entre sí (P.Ej. el número -1 representa al conjunto 2-3, 3-4 … 765-766, etc.).
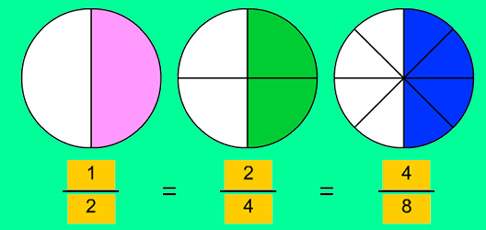
- números fraccionarios: en este caso cada número representa una cantidad infinita de pares de números enteros, en este caso relacionados por la división (a/b), y que suelen expresarse utilizando una coma tras la parte entera, seguida por los decimales. Así, el número 0,5 representa el conjunto infinito de pares de números en los que el numerador es la mitad del denominador a/b = 1/2 ; 2/4 ; 3/6 … 14/28; etc.
Cada conjunto de números se construye a partir del conjunto anterior, añadiendo relaciones nuevas entre los números. Podéis encontrar una explicación más detallada en Sangaku.com. De la misma manera, para más detalles sobre los números fraccionarios te recomiendo la entrada de EcuRed.
Vamos entonces con la propiedad de los números fraccionarios que explica la manera de calcular los porcentajes.
Cualquier porcentaje (A%) no es más que una manera de expresar la fracción A/100. Pero, como acabas de ver, una fracción es sólo uno entre infinitos pares de números equivalentes (numerador/denominador). Todos ellos son pares de números que guardan la misma relación entre sí. Por eso el 50 por ciento (50/100) de algo es lo mismo que
22/44 = 40/80 = 3/6 = 1/2 …
todos ellos representados por el número decimal 0,5.
Y ahora es importante entender la relación entre los pares de números que componen dos fracciones equivalentes. Lo que las caracteriza es que todas ellas pueden obtenerse a partir de una sola de ellas. La única condición es que multipliquemos por el mismo número arriba y abajo, es decir, tanto el «numerador» como el «denominador»:
Así que cuando conocemos una relación entre dos números con el 100 en la parte de abajo (el denominador) siempre podremos encontrar otra equivalente de la que sólo conocemos uno de los dos números, averiguando qué número es el que debe multiplicar arriba y abajo esa otra relación.
lo que nos vuelve a la misma situación que hemos visto arriba, cuando he explicado cómo se aplica la regla de tres.
En fin, se trata de practicar, así que prueba con estos ejercicios a ver si te da el mismo resultado:
¿cuál es el 17% de 4.000?
17/100 = x/4000 x= 17 * 4.000/100 = 680
¿qué tanto por ciento de un total de 30 millones de coches son los 6 millones de coches de color gris?
x/100 = 6/30 —-> x = 6 * 100/30 = 600/30 = 20 (son el 20%)
Cuánto me cuesta un interés del 2% anual de un préstamo de de 5.000 euros durante un año.
2/100 = x/5.000 —-> x= 2*5.000/100 = 10.000/100 = 100 (los intereses del préstamo te cuestan 100€)
Música en ApdD: Jamm Session with Devon Stixx Taylor, Rico Nichols, Domi, Bubby, Freaky Rob, Roland Gajate, Xavier feat Kaz



Como realizo una fracción 87 1/2 % de ______ =413
Me gustaMe gusta
Si me presto de un banco 12.000 y el interés es de 1.7al año cuanto estaria pagando al año con todo el interés.
Me gustaMe gusta
un articulo con la mejor información y que me ayudo mucho
Me gustaMe gusta
Excelente artículo, lo felicito. 👍
Tengo una duda. De donde salen los valores 10 y 15 que coloca en las en la ecuación y que no dan en el enunciado?. Gracias por responder
4/1 = x/10
2/3 = x/15
Me gustaMe gusta
Gracias Antonio por tus palabras. Tienes toda la razón al preguntar, porque hay un error en el enunciado. Yo lo he corregido, pero echa un vistazo a ver si ahora sí te parece lógico. un saludo y gracias por usar ApdD
Me gustaMe gusta
x=harina que tenemos que poner i no sabemos ?
x/10 azúcar que hemos puesto=3/2=x=10*3/2=30/2=15
Me gustaMe gusta
si tengo $457,391,00
si lo pongo de la siguiente manera
cual es el porcentaje
88.000.00 = %
88.000.00 = %
88,000.00 = %
88.000.00 = %
88.000.00 = %
17.392.00 = %
Me gustaMe gusta
Genial artículo, gracias
Me gustaMe gusta
Post muy bueno, gracias
Me gustaMe gusta
Muy buen articulo. Muy detallado el calculo.
Me gustaMe gusta
Hola me mandaron a calcular el porcentaje de población y casos hasta ahora, ejemplo Población= 4.199.165 y los casos de ese estado=7.469 osea multiplico casos x población y luego divido por 100 y redondeo el resultado? Ayuda please 😥
Me gustaMe gusta
Muy buen artículo . Creo que hay un error en
» ? admin/10 analis», según el enunciado sería
«40 admin/?analis».
Y en línea que le sigue, hay el mismo error
Saludos
Me gustaMe gusta
Hola Antonio, gracias por el comentario. Pero no hay error alguno, la igualdad entre dos razones permite despejar la incógnita sea el numerador o el denominador. El caso que comentas es un buen ejemplo, y puedes verlo sin hacer cálculo alguno, sólo de cabeza. Cambia analistas por euro; si 4 admin cuestan un euro, cuántos analistas tendrás con 10 euros? Saludos y gracias de nuevo
Me gustaMe gusta
Un artículo estupendo, me ha sido de gran utilidad, muchas gracias.
Me gustaMe gusta